第一台会下棋的机器　　　在1769年，匈牙利工程师巴朗·沃尔夫冈·凡·坎比林(Baron Wolfgang von Kempelen)为奥地利皇后做了一台会下国际象棋的机器来消遣。这是一个外形呆板的机械装置，不过它的出色棋力来自有一名象棋高手巧妙地藏在机器里的。所以这台会下棋的“机器”是个冒牌货。(如图)

[align=center]

[/align]

　

图灵的“纸上机器”

第一个棋弈程序写于电脑被真正发明之前，这是一个非常有趣的事实。它是由一名想象力丰富的人所编写的，他知道可编程电脑即将出现，一旦发明出来，就有下棋的能力。这位先生就是阿伦·图灵(Alan Turing)，有史以来最伟大的数学家之一。图灵的伟大成就是领导专家小组破译了纳粹德国的“谜”密码，因此对第二次世界大战的决定性结束作出了贡献。他对国际象棋非常感兴趣，不过他尽管智力超群并且下了很大工夫在学棋上，他还是一个蹩脚的棋手。战争结束不久，他就写下了能够让机器下棋的指令。由于当时还没有一台机器能够执行这些指令，于是他就自己执行，充当一个“人类CPU”，每走一步需要半个多小时【译注：所谓“自己执行”，即图灵根据他所写的算法去运算，严格根据运算得出的结果去走棋】。这里有一局棋，图灵的“纸上机器”输给了同事：

[align=center]图灵的“纸上机器”——Alick Glennie

[/align]

[align=center]曼彻斯特 1952

[/align]

1.e4 e5 2.Nc3 Nf6 3.d4 Bb4 4.Nf3 d6 5.Bd2 Nc6 6.d5 Nd4 7.h4 Bg4 8.a4 Nxf3+ 9.gxf3 Bh5 10.Bb5+ c6 11.dxc6 0-0 12.cxb7 Rb8 13.Ba6 Qa5 14.Qe2 Nd7 15.Rg1 Nc5 16.Rg5 Bg6 17.Bb5 Nxb7 18.0-0-0 Nc5 19.Bc6 Rfc8 20.Bd5 Bxc3 21.Bxc3 Qxa4 22.Kd2? [22.h5 本可得象] 22...Ne6 23.Rg4 Nd4? [23...Rxb2! 24.Bxb2 Rxc2+]　24.Qd3 Nb5　25.Bb3 Qa6 26.Bc4 Bh5 27.Rg3 Qa4 28.Bxb5 Qxb5 29.Qxd6 Rd8 0-1.　申朗的策略　　　贝尔实验室的克劳迪·申朗(Claude Shannon)是和图灵同时代的另一位伟大的数学家，他一直在探索教电脑下棋。他认识到问题在于棋步数量大得可怕，因此把搜索所有棋步的“A策略”和剔除某些变化路线的“B策略”区分开来。如今我们也区分“强行搜索”和“选择搜索”程序，尽管所有强大的程序或多或少属于前者。　国际象棋代替核弹　　　战争期间美国在新墨西哥州的阿拉莫斯建立了一个巨大的实验室，它的主要目的就是发展核武器。要正确执行触发链式反应的内部爆炸需要数量巨大的计算。

1946年美籍匈牙利数学家约翰·凡·诺依曼(John von Neumann)被指派设计一台强大的计算机器以加快工作进度的任务。到了1950年，一台叫“MANIAC一号”的巨型机被交付使用(图左)，它内装有数千个电子管和开关，每秒能执行10,000条指令。它也可以编程。科学家并不马上用它来设计核弹，而是先试验一下这台机器，而首先做的事情之一就是编写一个下棋的程序。这是一个缩小的6x6棋盘，没有象。虽然这么简化了但程序要搜索四层的深度就需要12分钟【译注：四层相当于当前局面双方各两步】，如果加上象，就需要3个小时。

　　50年代中期，这台机器下了三局棋。第一局是自己对自己，白胜。第二局是对一位让王后的强棋手，这局棋进行了10个小时，结果人类大师胜。第三局机器的对手是一位刚学棋一个星期的的年轻姑娘，结果程序23回合得胜。这是在智力博弈中人类首次负于电脑。　国际象棋和数学　　　程序下棋遇到的主要难题是所包含的棋步数量实在太多太多了。平均每个局面大约有40步符合规则的着法。如果你对每步着法都考虑应着就会遇到40 x 40 = 1600个局面。这意味着两层(ply，一层为半步棋)之后，单一步棋就会出现1600个不同的局面，而两步之后是250万个，三步之后是41亿个。平均一局棋大约走40步，于是所有可能局面就有10的128次方个，这个数字远远多于已知宇宙世界的原子总数目(大约10的80次方)！　　很显然没有一台电脑或其它机器可以搜索全部可能的着法来下棋，但人类也不行呀？唯一的问题是机器要达到人类的策略水平，需要搜索多深的深度。早期的电脑可以每秒产生和评价大约500个局面，或者在比赛中三分钟内对每步计算90,000个可能。意思就是它们仅能搜索三层的深度(即一步半)，这是很低的水平了，相当于新手。要搜索多一层需要每秒计算大约15,000个局面，也就是要快30倍。但即使能搜索四层也很浅薄，因此似乎电脑不可能达到大师级水平？　Alpha-beta算法　　　第一个突破出现在1958年，匹兹堡大学的三位科学家奈维尔、肖恩和西蒙有重大发现：可以从搜索树中剔除相当大的部分而不影响最后结果，他们把这叫Alpha-beta算法。很重要指出的是，这是一个纯数学领域的技巧，独立于任何国际象棋知识而生效。

[align=center]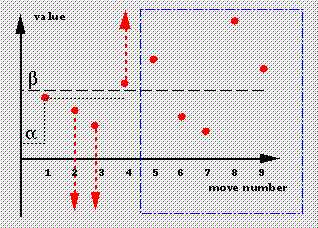

[/align]

[align=center]Alpha-Beta算法示意图1

[/align]　　　我们很粗略地描述一下Alpha-beta算法：比方说电脑已经完成评价一步棋，开始计算第二步棋。一旦单个变化显示返回的值低于第一步棋的值，就可以立即中止这个搜索。我们不需要精确知道第二步棋究竟有多差，程序会明确选择第一步棋。　

[align=center]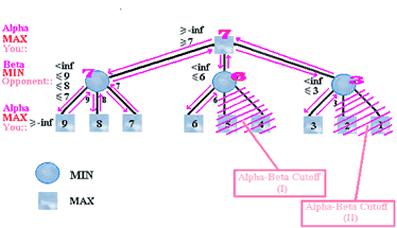

[/align]

[align=center]Alpha-Beta算法示意图2

[/align]

　　除非另有需要，当只搜索数目的平方根那么多局面时，Alpha-beta算法产生的结果和完全搜索是一样的。早期的电脑突然间也能向前看五至六层了，到了70年代最快的电脑可以搜索七层，棋力令人瞩目了。但即使使用Alpha-beta算法，要搜索深一层还是需要提高5倍速度。数目的指数爆发性增长再次赶上程序设计者。　硬件尤物　　　电脑科学家肯·汤普森(Ken Thompson，下图左)觉得不能等待快5-25倍的百万美元级超级电脑来用于提高下棋能力。他和贝尔实验室的同事一起决定建造一台专门用途的机器，使用了价值大约20,000美元的几百个芯片。他们把这台机器叫做“尤物”(belle，下图右)，它只会下国际象棋。它能够每秒搜索大约18万个局面(而当时的超级电脑只能搜索5000个)。“尤物”在比赛中可以搜索八至九层那么深，因此可以和大师同场竞技。从1980年到1983年它赢得了世界电脑国际象棋和所有其它电脑竞赛冠军，直到被价钱贵上千倍的克雷X-MPs巨型机(Cray X-MPs)取代为止。

[align=center]

[/align]下棋的芯片　　　80年代中期，电脑科学家、卡梅隆大学的汉斯·贝利纳(Hans Berliner，下图左)教授接手肯·汤普森放下的工作。贝利纳曾经是世界国际象棋通讯赛冠军，他制造了一台硬件型的机器叫“高技术”(HiTech)，他和他的研究生一起研究可拔插芯片。装有64个并行芯片的“高技术”差点赢得了1986年的世界电脑国际象棋冠军(冠军是克雷)。随后贝利纳的几个学生包括华人许锋雄等自行研究叫“芯测”的机器，后来则是“深思”(Deep Thought)。它只花5000美元但每秒搜索50万个局面。许锋雄(下图右)等后来加入了IBM，和其他人合作制造了IBM现在的“深蓝”(Deep Blue)。

[align=center]

[/align]深蓝　　　加里·卡斯帕罗夫在费城和纽约面对的这台电脑包括一个装备大量专门用以进行高速运算芯片的IBMSP/2服务器，每个芯片每秒能处理2-3百万个局面。使用超过200个这种芯片，整个程序的速度达到了每秒处理2亿个局面。　　棋弈机器每秒能处理2亿个局面意味着什么？肯·汤普森，“尤物”之父(也是Unix和C语言之父)，在80年代对搜索深度和棋力提高之间的关系做了非常有意义的试验。他让“尤物”自己跟自己下，但只有一方的搜索深度不断增加，平均每增加一个搜索深度可大约换算成200个国际象棋等级Elo分。于是，“尤物”搜索四层其水平大约是1230分，搜索到九层它的水平达到了2328分。延伸这条曲线，到了顶端会变平缓，可以计算出搜索深度达到十四层时，就达到了世界冠军的程度即2800分。(如下图，横坐标是搜索层数，纵坐标是国际等级分。上部横线是卡斯帕罗夫的分数作参考，A线表示对电脑水平的乐观估计，B线表示悲观估计，C线表示现实估计)

[align=center]

[/align]

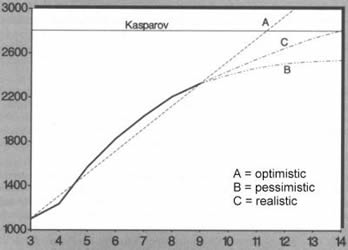
[align=center]搜索深度和棋力关系曲线图

[/align]　　　专家的结论是：要与人类世界冠军争夺冠军，必须做一台每秒运算10亿次的电脑(搜索到十四层的深度)。深蓝接近了，但还达不到。【译注：注意这里搜索到十四层的深度，应该是指规定比赛分配时间内对所有回合而言。否则对一步棋不限制时间地搜索，或者对一些简单局面的搜索，要达到十四层对当今众多高速电脑来说实在不是难事。】　　当然，程序的质量也扮演重要角色。今天的顶级个人电脑程序象Fritz和Junior可以达到并超过每秒处理50万个局面。它们事实上已经超过2600分的水平，可以对抗除世界前100名棋手之外的任何人。在快棋战里人类只有大约前十几位可以胜任，而在超快棋里大概只有两、三名人类棋手能过关。【译注：也可见，每升高等级而要求的运算速度的提高绝不是仅仅直线式的，而是指数式的。所以每秒计算50万次就达到2600分的特级大师水平，但要达到2800分，根据上面估算则需要每秒计算10亿次之多。】　挑战所有开局　　　电脑棋力的一个重要方面是下棋时使用广阔的开局库。多少代人类大师的知识积累和经验可以轻易地储存在硬盘上并且在开局阶段采用。即使是个人电脑程序也懂得几千万个开局局面，并且对这些局面的每一个都有完全的统计(比如出现过那些着法、用哪些着法胜过、使用过的人有多少，等等)。程序经常是连走15到20步之后才第一次需要计算。如果没有从这些人类的开局知识精华中受益，程序将实力大减。　　当电脑从数目庞大的、从国际象棋历史积累下来的开局知识中取得坚实优势之时，它们也从对局的另一端搜索中受益。　残局数据库　　　这又是那位影响力到处有的肯·汤普森充当了研究先锋。他在80年代就开始生成和储存棋盘上剩四至五子的所有符合规则的残局。一个典型的五子残局，比如王双象对王单马，包含总数121万个局面。加上一只移动不连续的兵，这个数字增加到335万。汤普森编写程序产生所有符合规则的局面并计算出每个残局可能的强制变化。他还以一种方式把结果压缩，使得一张标准的CD-ROM能存放大约20个残局。【译注：原文没有提另一位对残局数据库的发展作出重大贡献的Nalimov。】　　电脑使用这些残局数据库，可以把每个残局走得绝对完美，就象上帝一样。对于棋盘出现子力及数目符合的任何局面，电脑可以立刻知道该胜、该和还是该负，并且知道要多少步。它经常宣布15步棋之后取胜或将死，而执输棋那一种颜色的则能够最优化地防守【即在必然被将死前每一步防守都尽力最优化】。深蓝使用了汤普森的残局数据库，而象Fritz这样的个人电脑程序也把它们贯彻在搜索树中。这些对棋力有什么影响还有待观察。有些五子的残局极之困难甚至对于人类来说难以掌握，但这些五子残局对于汤普森正在努力的六子残局来说只是小巫见大巫，在某些六子局面里，要取胜不得不进行超过200步的计算【译注：当然这是在纯电脑国际象棋领域来说，实际上人类走残局，经验和知识比重很大，有很多棋根本不用考虑就知道该怎么样走。但电脑却是“一丝不苟”地全部去算。所以，从数字上比意义还不大】。自然硬件技术的发展是有利于电脑的，汤普森的六子残局，每个包含80到200亿个局面，刚好能够压缩进一张DVD。【译注：高端应用情况不得知，而普遍应用于个人电脑程序的Nalimov残局数据库，全部四子残局大约占30MB储存，全部五子残局需要7GB，至于六子残局，目前可见的只是一些比较简单局面而且一只兵也没有的，因为兵会升变，复杂性巨增，如果加上则相当时期内一般电脑的硬盘难以承受，别忘了增长不是直线而是指数式的。】　　好在，局面数量更大得不可思议的七子残局，离产生依然很遥远。更好在的是，对局的两端即开局和残局，永不可能接在一起。是啊，假如看到一台电脑走了 1.e4 然后宣布40步棋之内将死，这就太难以让人接受了。但是电脑在比赛中稳定战胜人类世界冠军大概只是时间问题，若干年或若干十年之后……　　【译注：1997年深蓝在“回敬赛”中战胜棋王卡斯帕罗夫，但那次的场外不明朗因素太多，结果未必有说服力，何况注意到两次比赛总成绩其实还是卡帕罗夫以6.5-5.5战胜深蓝。2002年10月的克拉姆尼克对Deep Fritz人机大战，不明朗因素又有点倾向于克拉姆尼克，以至舆论认为电脑机会不大，且到时看。卡斯帕罗夫本人当初认为电脑真正稳定战胜人类世界冠军要到2010年，汤普森则认为可能要到2018年。有趣的是包括贝利纳、许锋雄等人在上世纪90年代初认为电脑在1994年就可以达到这点的。】